动态规划解 LCR191.按规则计算统计结果

题目描述

LCR 191. 按规则计算统计结果

为了深入了解这些生物群体的生态特征，你们进行了大量的实地观察和数据采集。数组 arrayA 记录了各个生物群体数量数据，其中 arrayA[i] 表示第 i 个生物群体的数量。请返回一个数组 arrayB，该数组为基于数组 arrayA 中的数据计算得出的结果，其中 arrayB[i] 表示将第 i 个生物群体的数量从总体中排除后的其他数量的乘积。

示例 1：

输入：arrayA = [2, 4, 6, 8, 10]
输出：[1920, 960, 640, 480, 384]

提示：

• 所有元素乘积之和不会溢出 32 位整数
• arrayA.length <= 100000

解题思路

累乘后除

当然其实首先考虑就是先累乘所有数值的乘积，然后除以当前元素的值，这样就能得到当前元素排除后的乘积。但是这种方法需要注意除数为 0 的情况，因为除数不能为0，并且当有多个0的时候，结果也会不一样。针对 0 的情况，还是需要单独处理。最后其实也能得到一个 0ms 的结果：

func statisticalResult(arrayA []int) []int {
    if len(arrayA) == 0 {
        return arrayA
    }

	var sum int = arrayA[0]
	var hasZero int = 0
	for i := 1; i < len(arrayA); i++ {
		if arrayA[i] != 0 {
			sum = sum * arrayA[i]
		} else {
            hasZero++
        }
	}

	var arrayB []int = make([]int, len(arrayA))
	for i := 0; i < len(arrayA); i++ {
		if arrayA[i] != 0 {
			if hasZero > 0 {
				arrayB[i] = 0
			} else {
				arrayB[i] = sum / arrayA[i]
			}
		} else {
            if hasZero > 1 {
                arrayB[i] = 0
            } else {
    			arrayB[i] = sum
            }
		}
	}

	return arrayB
}

毕竟也没有明确说不能用除法……

不使用除法的暴力解

首先用暴力法解决这个问题，遍历数组，每次将数组中的一个元素排除，然后计算剩余元素的乘积，最后将结果存入结果数组中。这种方法的时间复杂度为 O(N^2)，不符合题目要求。

func statisticalResult(arrayA []int) []int {
	var results []int = make([]int, len(arrayA))

	for i := 0; i < len(arrayA); i++ {
		sum := 1
		for j := 0; j < len(arrayA); j++ {
			if j == i {
				continue
			}

			sum = sum * arrayA[j]
		}
		results[i] = sum
	}

	return results
}

结果也很显然，运行超时，时间复杂度太高。

动态规划解

然后考虑其实有大量的重复计算，比如计算 arrayA[1] 排除后的乘积，需要计算 arrayA[0] 和 arrayA[3] 的乘积，而计算 arrayA[2] 排除后的乘积，也需要计算 arrayA[0] 和 arrayA[3] 的乘积。所以可以考虑用空间换时间，用两个数组分别存储每个元素左边的乘积和右边的乘积，然后将两个数组相乘即可。另外，左边的乘积可以从左往右计算，右边的乘积可以从右往左计算，这就是动态规划的思想。把计算分为n个阶段，每个阶段的计算结果可以用来计算下一个阶段的结果。最后将两个数组相乘即可得到最终结果。

func statisticalResult(nums []int) []int {
	n := len(nums)
    if n == 0 {
        return nums
    }

	results := make([]int, n)
	leftProducts := make([]int, n)
	rightProducts := make([]int, n)

	leftProducts[0] = 1
	rightProducts[n-1] = 1

	for i := 1; i < n; i++ {
		leftProducts[i] = leftProducts[i-1] * nums[i-1]
		rightProducts[n-1-i] = rightProducts[n-i] * nums[n-i]
	}

	for i := 0; i < n; i++ {
		results[i] = leftProducts[i] * rightProducts[i]
	}

	return results
}

最后在 LeetCode 上提交，通过测试，但是遇到一个很奇怪的问题，用上面的代码提交，耗时显示是 4ms。

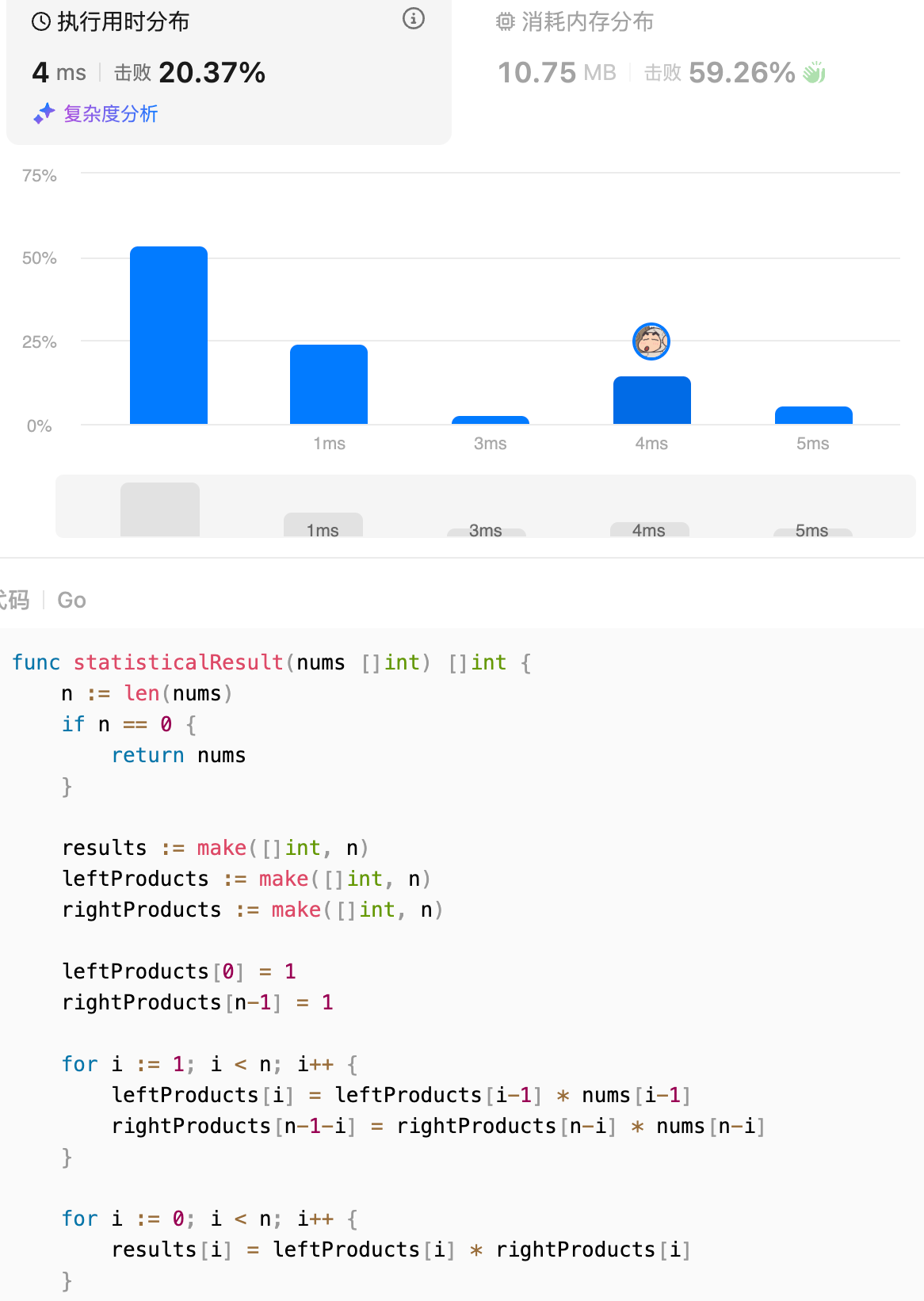
但是如果不把 leftProducts 和 rightProducts 的计算放在一起，而是分开计算，耗时显示是 1ms。

func statisticalResult(nums []int) []int {
	n := len(nums)
	if n == 0 {
		return nums
	}

	results := make([]int, n)
	leftProducts := make([]int, n)
	rightProducts := make([]int, n)

	leftProducts[0] = 1
	rightProducts[n-1] = 1

	for i := 1; i < n; i++ {
		rightProducts[n-1-i] = rightProducts[n-i] * nums[n-i]
	}

	for i := 1; i < n; i++ {
		leftProducts[i] = leftProducts[i-1] * nums[i-1]
	}

	for i := 0; i < n; i++ {
		results[i] = leftProducts[i] * rightProducts[i]
	}

	return results
}

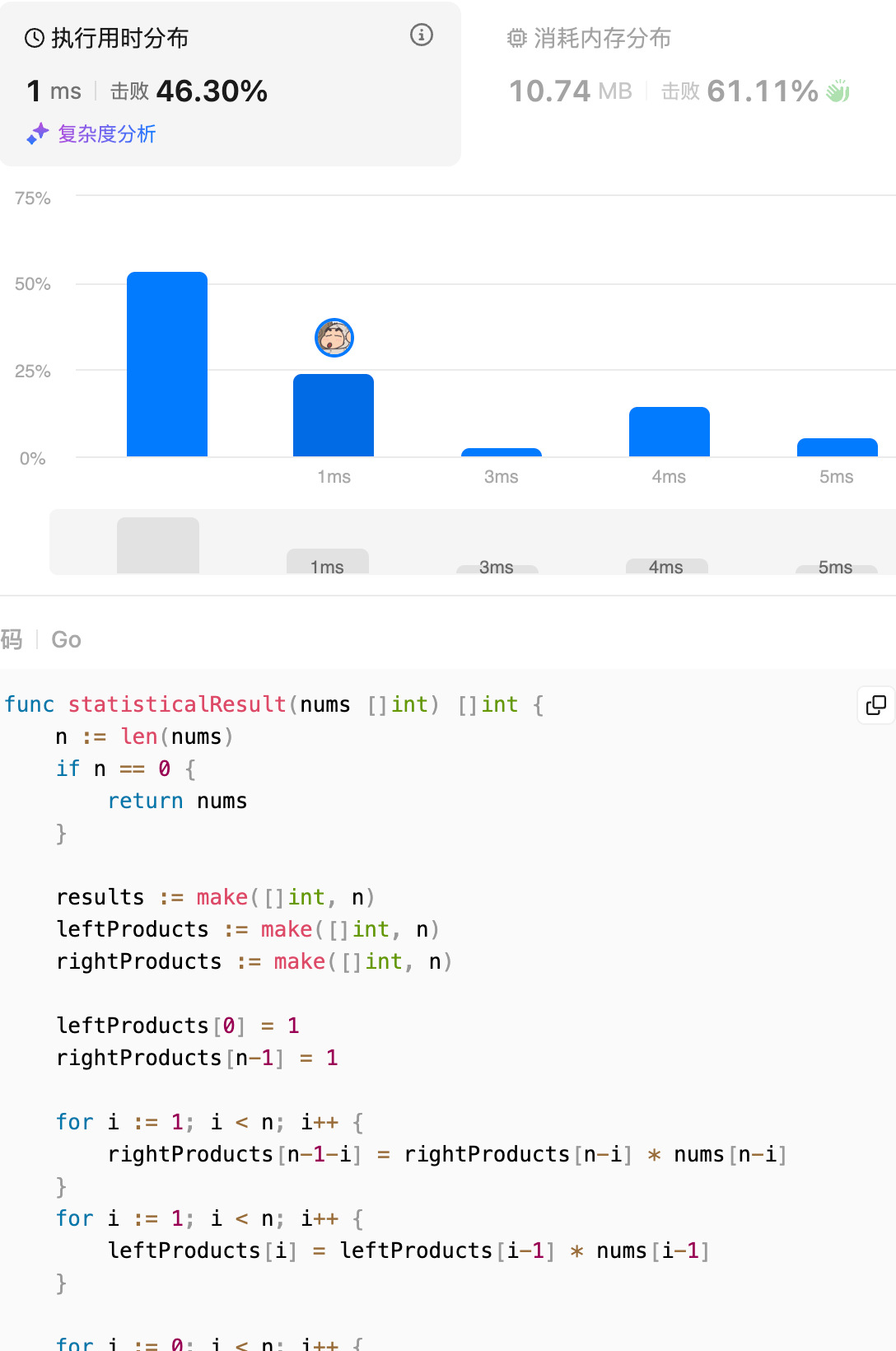
然后我突然发现，该函数的传入变量名被我改掉了，应该是 arrayA，而不是 nums。然后我把变量名改回来，再次提交，耗时显示是 0ms。

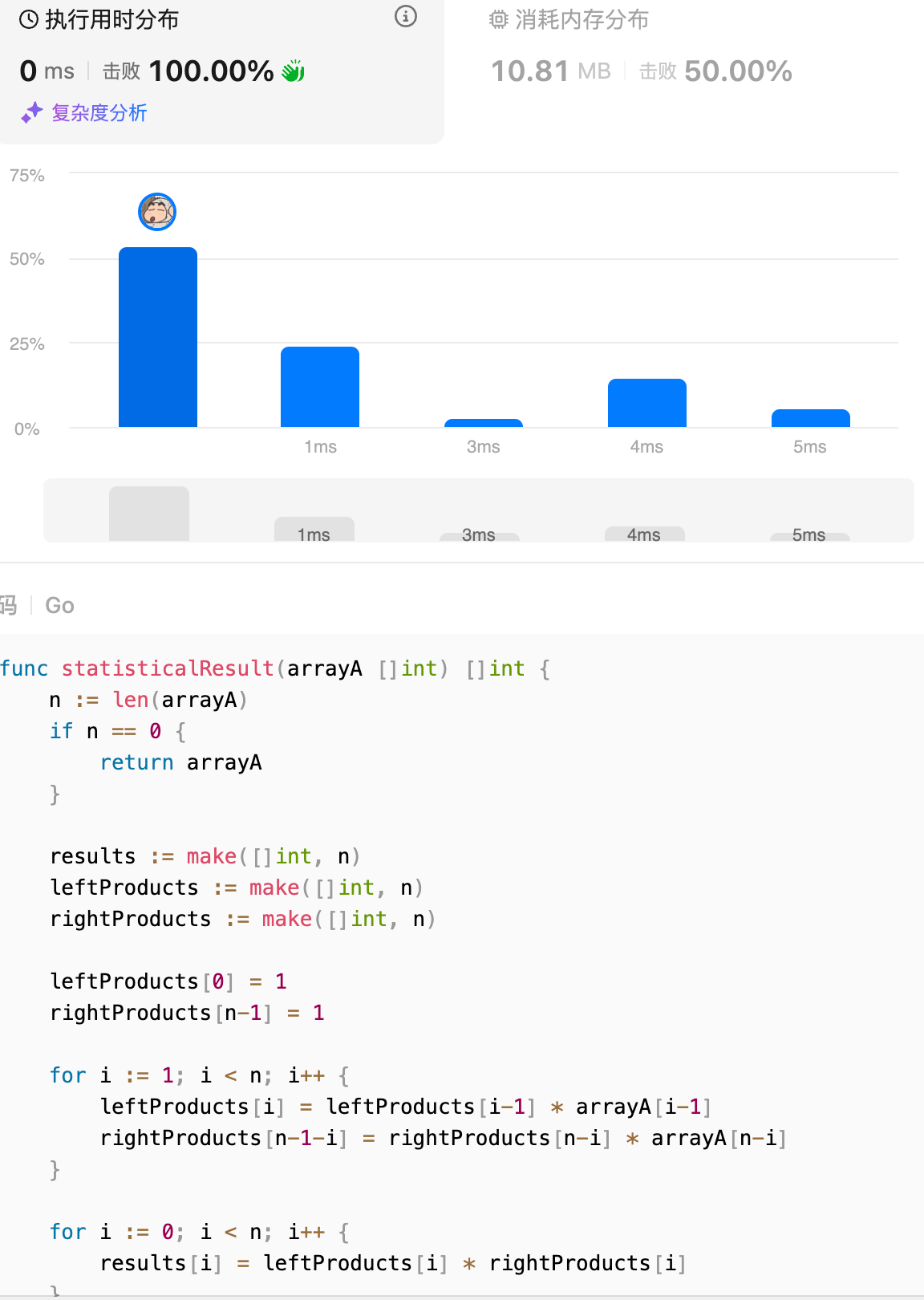
而且这三次提交的内存消耗还不一样，所以合理怀疑 LeetCode 的测试环境做过一些特定优化，不过这个问题不影响解题思路，只是有点奇怪。