题目

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

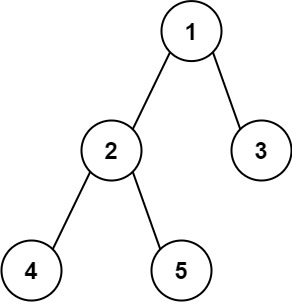
diamtree.jpg

输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

树中节点数目在范围 [1, 104] 内
-100 <= Node.val <= 100

解题思路

二叉树基本上第一反应就是递归，求直径的思路就是：

  • 左子树为空：“右子树根节点到叶子节点的路径长度”和“右子节点为根结点的二叉树直径”的最大值
  • 右子树为空：“左子树根节点到叶子节点的路径长度”和“左子节点为根结点的二叉树直径”的最大值
  • 左子树和右子树都不为空：“根节点到左子树叶子节点的距离+根节点到右子树叶子节点的距离”，“左子节点为根结点的二叉树直径”和“右子节点为根结点的二叉树直径”的最大值

而要求以某个节点到叶子节点的最大路径长度，实际上就是求该节点的左子树和右子树的最大深度。这又是一个递归问题。所以可以定义一个函数 longestPathFromNode，它的参数是一个节点，返回该节点到叶子节点的最大路径长度。

1
2
3
4
5
6
7
func longestPathFromNode(node *TreeNode) int {
	if node == nil || node.Left == node.Right {
		return 0
	}

	return max(longestPathFromNode(node.Left), longestPathFromNode(node.Right)) + 1
}

然后就可以编写函数 diameterOfBinaryTree，它的参数是一个节点，返回该节点的直径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func diameterOfBinaryTree(root *TreeNode) int {
	if root == nil {
		return 0
	}

	if root.Left == root.Right {
		return 0
	}

	if root.Left == nil {
		return max(longestPathFromNode(root.Right)+1, diameterOfBinaryTree(root.Right))
	}

	if root.Right == nil {
		return max(longestPathFromNode(root.Left)+1, diameterOfBinaryTree(root.Left))
	}

	return max(longestPathFromNode(root.Left)+longestPathFromNode(root.Right)+2, max(diameterOfBinaryTree(root.Left), diameterOfBinaryTree(root.Right)))
}

其中 root.Left == root.Right 的判断是如果当前节点的左右子树都为空，则返回 0。

用测试数据验证一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
func arrayToBinaryTree(arr []interface{}) *TreeNode {
	if len(arr) == 0 {
		return nil
	}

	root := &TreeNode{Val: arr[0].(int)}
	queue := []*TreeNode{root}
	i := 1

	for i < len(arr) {
		current := queue[0]
		queue = queue[1:]

		// left child
		if i < len(arr) && arr[i] != nil {
			leftNode := &TreeNode{Val: arr[i].(int)}
			current.Left = leftNode
			queue = append(queue, leftNode)
		}
		i++

		// right child
		if i < len(arr) && arr[i] != nil {
			rightNode := &TreeNode{Val: arr[i].(int)}
			current.Right = rightNode
			queue = append(queue, rightNode)
		}
		i++
	}

	return root
}

func main() {
	arr := []interface{}{4, -7, -3, nil, nil, -9, -3, 9, -7, -4, nil, 6, nil, -6, -6, nil, nil, 0, 6, 5, nil, 9, nil, nil, -1, -4, nil, nil, nil, -2}
	root := arrayToBinaryTree(arr)

	println(diameterOfBinaryTree(root))
}

能通过测试，输出结果为 8。其实细想一下，每一个直径一定会有一个顶节点。所以可以遍历整个二叉树，以每一个节点为顶节点来计算直径。而每一个节点的直径都可以通过左右树的深度相加来求得。

遍历二叉树的方式有很多种，实现上一般是借助栈或者递归来实现。考虑上面编写的函数 longestPathFromNode，其用于计算某个节点到叶子节点的最大路径长度。在递归的过程中，其实已经遍历了整棵树。我们可以在这个函数中，顺便计算出当前节点的直径。这样就不需要再遍历一次了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func diameterOfBinaryTree(root *TreeNode) (maxDiameter int) {
	if root == nil || root.Left == root.Right {
		return
	}

	var longestPathFromNode func(node *TreeNode) int
	longestPathFromNode = func(node *TreeNode) int {
		if node == nil {
			return 0
		}

		left, right := longestPathFromNode(node.Left), longestPathFromNode(node.Right)
		maxDiameter = max(maxDiameter, left+right)

		return max(left, right) + 1
	}

	longestPathFromNode(root)

	return
}

这样就可以在一次遍历中计算出整棵树的直径了。