题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

tree

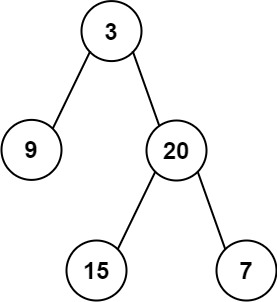
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

  • 1 <= inorder.length <= 3000
  • postorder.length == inorder.length
  • -3000 <= inorder[i], postorder[i] <= 3000
  • inorder 和 postorder 都由 不同 的值组成
  • postorder 中每一个值都在 inorder 中
  • inorder 保证是树的中序遍历
  • postorder 保证是树的后序遍历

解题思路

二叉树的话基本想法还是递归了，后序遍历的最后一个元素是根节点，找到根节点在中序遍历中的位置，然后就可以分割出左子树和右子树的中序遍历和后序遍历。如此递归构建一颗二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(inorder []int, postorder []int) (root *TreeNode) {
	if len(postorder) == 0 {
		return
	}

	root = &TreeNode{Val: postorder[len(postorder)-1]}

	if len(postorder) == 1 {
		return
	}

	if root.Val == inorder[0] {
		root.Right = buildTree(inorder[1:], postorder[:len(postorder)-1])
		return
	}

	if root.Val == inorder[len(inorder)-1] {
		root.Left = buildTree(inorder[:len(inorder)-1], postorder[:len(postorder)-1])
		return
	}

	inorderRootIdx, postRightStart := 0, 0
	leftNodeM := make(map[int]struct{})
	for inorder[inorderRootIdx] != root.Val {
		leftNodeM[inorder[inorderRootIdx]] = struct{}{}
		inorderRootIdx++
	}

	for _, ok := leftNodeM[postorder[postRightStart]]; ok; _, ok = leftNodeM[postorder[postRightStart]] {
		postRightStart++
	}

	root.Left = buildTree(inorder[:inorderRootIdx], postorder[:postRightStart])
	root.Right = buildTree(inorder[inorderRootIdx+1:], postorder[postRightStart:len(postorder)-1])

	return
}

这里的思路是先找到根节点，然后通过一个 map 来记录左子树的节点，方便在后序遍历中找到右子树的起始位置。这样就可以递归地构建二叉树。

看了题解后发现还有一种思路可以不使用 map，每次只分割出中序遍历的左右子树，然后优先构建右子树，这样就可以直接使用后序遍历的最后一个元素作为根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(inorder []int, postorder []int) *TreeNode {
	var build func(start, end int) *TreeNode
	build = func(start, end int) *TreeNode {
		if start > end {
			return nil
		}

		root := &TreeNode{Val: postorder[len(postorder)-1]}
		postorder = postorder[:len(postorder)-1]

		inorderRootIdx := 0
		for inorder[inorderRootIdx] != root.Val {
			inorderRootIdx++
		}

		root.Right = build(inorderRootIdx+1, end)
		root.Left = build(start, inorderRootIdx-1)
		return root
	}

	return build(0, len(inorder)-1)
}

这里代码更加简洁，直接在递归函数中处理后序遍历的数组，不需要额外的 map 来记录左子树的节点。每次递归时，先构建右子树，再构建左子树，这样就可以直接使用后序遍历的最后一个元素作为根节点（使用最后一个元素后去除该元素）。

更进一步，避免每次递归都需要遍历 inorder 数组来找到根节点的位置，可以使用一个 map 来记录中序遍历中每个元素的索引，这样可以在 O(1) 的时间复杂度内找到根节点的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func buildTree(inorder []int, postorder []int) *TreeNode {
	inorderIndexMap := make(map[int]int, len(inorder))
	for i, v := range inorder {
		inorderIndexMap[v] = i
	}

	var build func(start, end int) *TreeNode
	build = func(start, end int) *TreeNode {
		if start > end {
			return nil
		}

		root := &TreeNode{Val: postorder[len(postorder)-1]}
		postorder = postorder[:len(postorder)-1]

		inorderRootIdx := inorderIndexMap[root.Val]

		root.Right = build(inorderRootIdx+1, end)
		root.Left = build(start, inorderRootIdx-1)
		return root
	}

	return build(0, len(inorder)-1)
}