题目描述

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

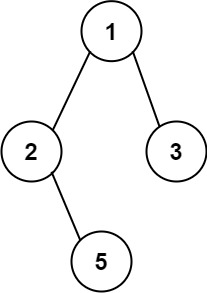
二叉树示例

输入：root = [1,2,3,null,5]
输出：[“1->2->5”,”1->3”]

示例 2：

输入：root = [1]
输出：[“1”]

提示：

  • 树中节点的数目在范围 [1, 100] 内
  • -100 <= Node.val <= 100

解题思路

基本想法还是递归了，走先序遍历，每次遇到有效节点就将节点值加入路径中，然后查看当前节点是否为叶子节点，如果不是则判断当前节点的左右子树是否存在，若存在则继续递归遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func binaryTreePaths(root *TreeNode) []string {
	paths := [][]string{[]string{}}
	var preOrderBinary func(node *TreeNode, idx int)
	preOrderBinary = func(node *TreeNode, idx int) {
		if node == nil {
			return
		}

        // 将当前节点值添加到路径中
		paths[idx] = append(paths[idx], strconv.Itoa(node.Val))

		if node.Left == nil {
			preOrderBinary(node.Right, idx)
			return
		}

		if node.Right == nil {
			preOrderBinary(node.Left, idx)
			return
		}

        // 代码走到这说明当前节点有左右子树，也就是在该节点处路径分叉了
        // 需要为右子树创建一个新的路径分支
		nIdx := len(paths)
		paths = append(paths, make([]string, len(paths[idx])))
		copy(paths[nIdx], paths[idx])

		preOrderBinary(node.Left, idx)
        // 用 nIdx 记录新路径的索引，而不是使用 len(paths) 直接获取，因为在递归过程中可能会多次调用 preOrderBinary，导致 len(paths) 变化。
		preOrderBinary(node.Right, nIdx)

		return
	}

	preOrderBinary(root, 0)
	ans := make([]string, len(paths))
	for i, ps := range paths {
		ans[i] = strings.Join(ps, "->")
	}

	return ans
}

上面的代码中，preOrderBinary 函数是一个递归函数，用于遍历二叉树并构建路径。它接受两个参数：当前节点 node 和当前路径的索引 idx。在每次递归调用时，都会将当前节点的值添加到对应路径中。如果当前节点是叶子节点（即没有左子树和右子树），则直接返回。如果当前节点有左子树或右子树，则继续递归遍历。

最后用 strings.Join 将每条路径连接成字符串，并返回所有路径的字符串切片。因为 strings.Join 会将切片中的元素用指定的分隔符连接起来，这里使用的是 "->" 作为分隔符。直接在递归的时候拼接路径字符串也可以，但需要特别判断是否需要加 -> 符号（开头不用加，后面需要），这样代码会更复杂。字符串拼接性能也不高，具体可以看 Go String 总结（LCR 182. 动态口令）。

总结

这里关键点就是要想到如何在递归过程中维护路径信息。通过在递归函数中传递路径的索引，可以在不同的递归层级中共享和更新路径信息，从而避免了在每次递归时都重新创建路径字符串的开销。

另外注意新路径分支的创建和索引的管理，确保在递归过程中不会混淆不同路径的内容。